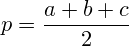Polttoaineen määrän laskenta tilasäiliössä

Sylinterinmuotoisen tankin sisältö

Säiliön säde cm:
Säiliön pituus cm:
Nesteen määrä cm:
Laskennan desimaalit:
0.1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0
Laske
1. Nesteen määrä litraa:9.38
2. Prosenttia kokonaismäärästä:37.1
3. Säiliön tilavuus:25.27

Ok, the solution is simple if you look at the picture. (If there are more than half of cylinder filled with liquid, we can compute air volume and subtract from total.)

Total volume of cylinder is
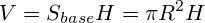
$V=S_{base}H=\pi R^2H$

So we need to find area of circle filled with liquid and multiply by height.
Filled area is sector area minus triangle area.
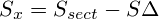
$S_x=S_{sect}-S{\Delta}$

Sector area is
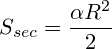$S_{sec}=\frac{\alpha R^2}{2}$ , where alpha is arc angle.

Arc angle is unknown yet. To find it, we draw vertical line from center of circle. It divides triangle to two right-angle triangles with hypotenuse equals to R and top cathet R-m.
Thus,
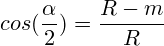
$cos(\frac{\alpha}{2})=\frac{R-m}{R}$
and
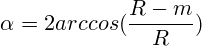
$\alpha=2arccos(\frac{R-m}{R})$

The top triange is isosceles. The sides equal to R. Let's find its base. The base is two times cathet from right-angle triangle, which is
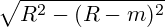
$\sqrt{R^2-(R-m)^2}$
according to pythagorean theorem.

Now, knowing all triangle sides we can compute its area using, for example, Calculator of area of a triangle using Hero's formula
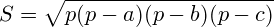
$S=\sqrt{p(p-a)(p-b)(p-c)}$
where
$p=\frac{a+b+c}{2}$